GH-01 Wasan
GH-01 Wasan

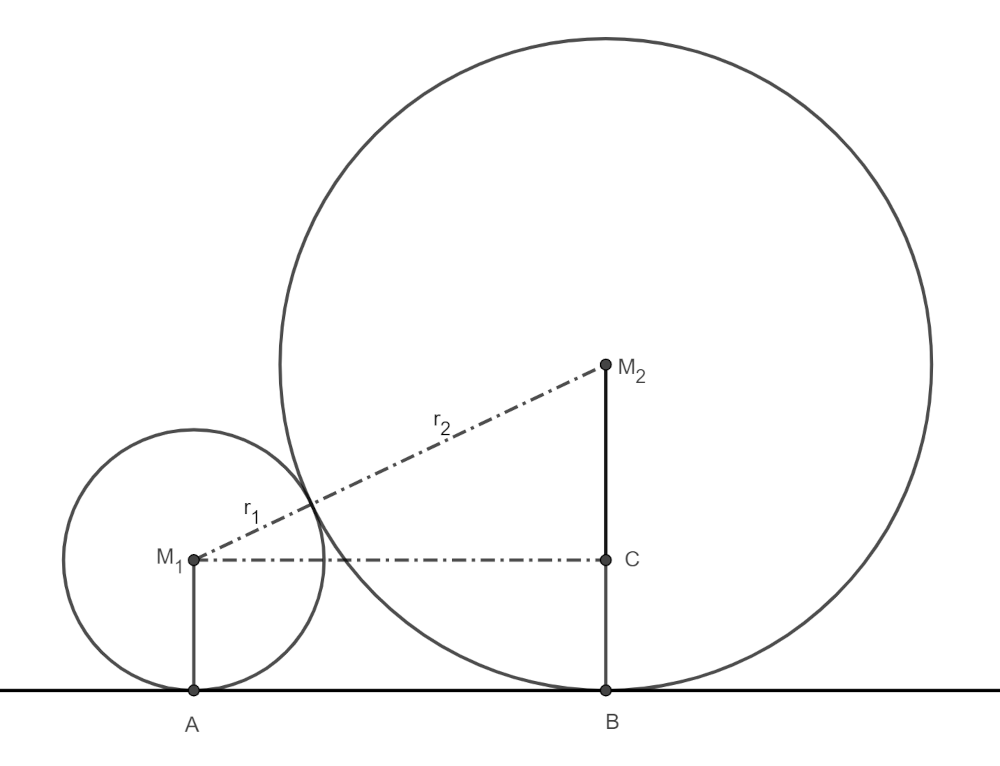
Twee cirkels, een rode en een blauwe, raken aan een lijn. Welke relatie bestaat er tussen de afstand van de twee raakpunten en de stralen van de cirkels?
Uitleg
Noem de stralen van de cirkels ( r_1 ) en ( r_2 ).
Pas de stelling van Pythagoras toe in ( Delta M_1M_2C ).
Dit geeft:
( (r_1+r_2)^2=(r_2-r_1)^2+M_2C^2 )
Uitwerken geeft:
( r_{1}^{2}+2r_{1}r_{2}+r_{2}^{2}=r_{2}^{2}-2r_{1}r_{2}+r_{1}^{2}+M_{2}C^{2} )
Daarom geldt:
( AB=M_1C=2 cdot sqrt{r_1r_2} )
