GH-05 Drie cirkels in een rechthoekige driehoek
GH-05 Drie cirkels in een rechthoekige driehoek
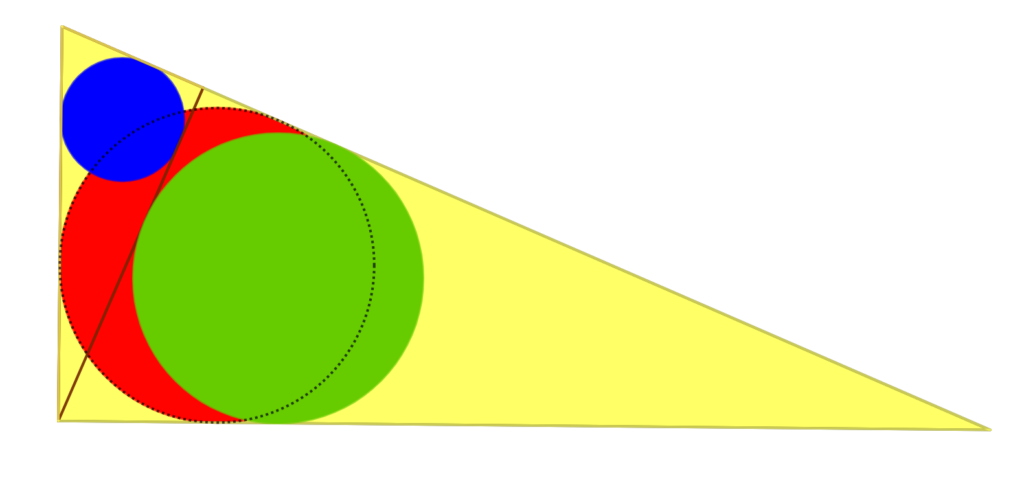
In een rechthoekige (gele) driehoek is een (rode) ingeschreven cirkel getekend. Uit het hoekpunt behorende bij de rechte hoek is een loodlijn op de overstaande zijde getekend. In de zo ontstane driehoeken zijn de ingeschreven cirkels getekend (een rode en een groene).
Wat is het verband tussen de stralen van de ingeschreven (rode, blauwe en groene) cirkels?
( r_{1}+r_{2}+r_{3}=h )
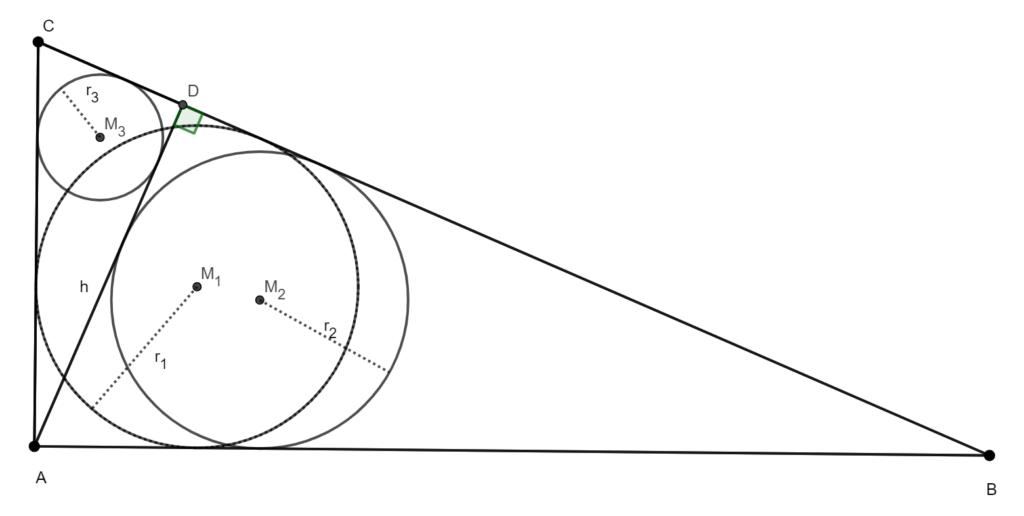
Hierbij zijn (r_{1} ), (r_{1} ) en (r_{1} ) de lengten van de stralen van de ingeschreven cirkels en h is de lengte van de hoogtelijn uit het hoekpunt met de rechte hoek.
Voor de lengte van de straal van de ingeschreven cirkel in een rechthoekige driehoek geldt de formule:
( r=frac{a+b-c}{2} )
Hierin is ( r ) de straal van de cirkel, ( a ) en ( b ) zijn de lengten van de twee rechthoekszijden en ( c ) is de lengte van de hypotenusa.
Passen we dit toe op de drie ingeschreven cirkels dan krijgen we:
( r_{1}=frac{AB+AC-BC}{2} )
( r_{2}=frac{AD+BD-AB}{2} )
( r_{3}=frac{AD+DC-AC}{2} )
Hieruit volgt: ( r_{1}+r_{2}+r_{3}=frac{AB+AC-BC+AD+BD-AB+AD+DC-AC}{2}=frac{-BC+h+BC+h}{2}=h ).
Dit is precies wat we moeten bewijzen!
