GH – Ingeschreven cirkel in een rechthoekige driehoek
GH – Ingeschreven cirkel in een rechthoekige driehoek

In een rechthoekige driehoek is een ingeschreven cirkel getekend. Geef een formule voor de lengte van de straal van deze cirkel
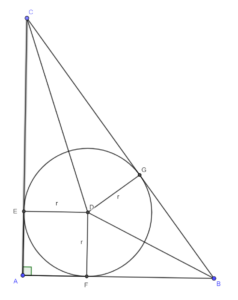
Te bewijzen
( r=frac{b+c-a}{2} )
Hierbij is r de lengte van de straal van de ingeschreven cirkel, a de lengte van de schuine zijde BC van de rechthoekige driehoek en b en c de lengte van de rechthoekszijden AC en AB.
In driehoek ABC geldt:
a = lengte van BG + lengte van CG = lengte van BF + lengte van CE . Dus geldt: ( a = c-r+b-r=c+b-2r ). Daaruit volgt: ( 2r=b+c-a ) en dus:
