GH-20 Twee cirkels
GH-20 Twee cirkels
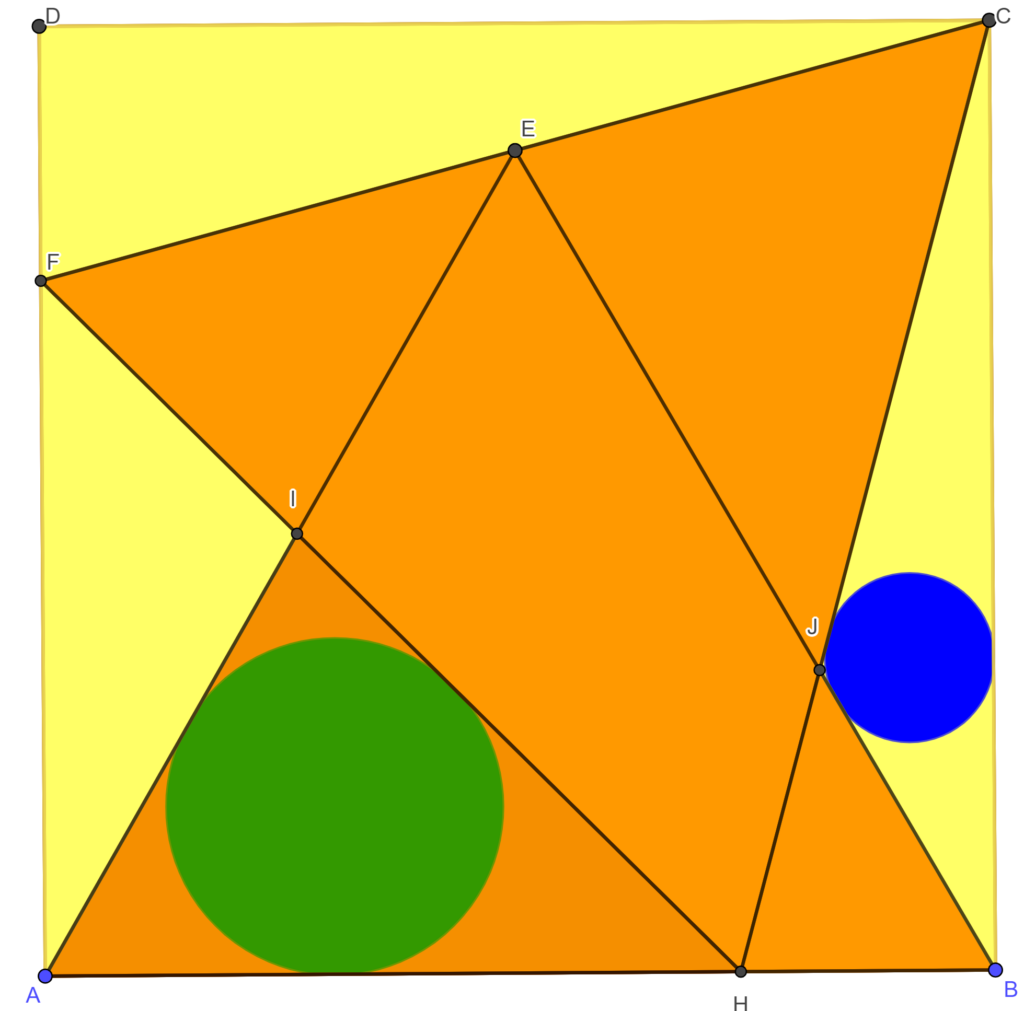
In een vierkant ABCD wordt een gelijkzijdige driehoek ABE getekend. De basis AB van deze gelijkzijdige driehoek valt dus samen met de zijde AB van het vierkant. De lijn door C en E snijdt de zijde AB in F. Er wordt een tweede gelijkzijdige driehoek CFH getekend, waarbij H een punt is op AB. Lijnstuk HF snijdt lijnstuk AE in I. Lijnstuk BE snijdt lijnstuk HC in J. In ΔAHI en in ΔBJC worden de ingeschreven cirkel getekend. Welk verband bestaat er tussen de grootte van de stralen van deze cirkels?
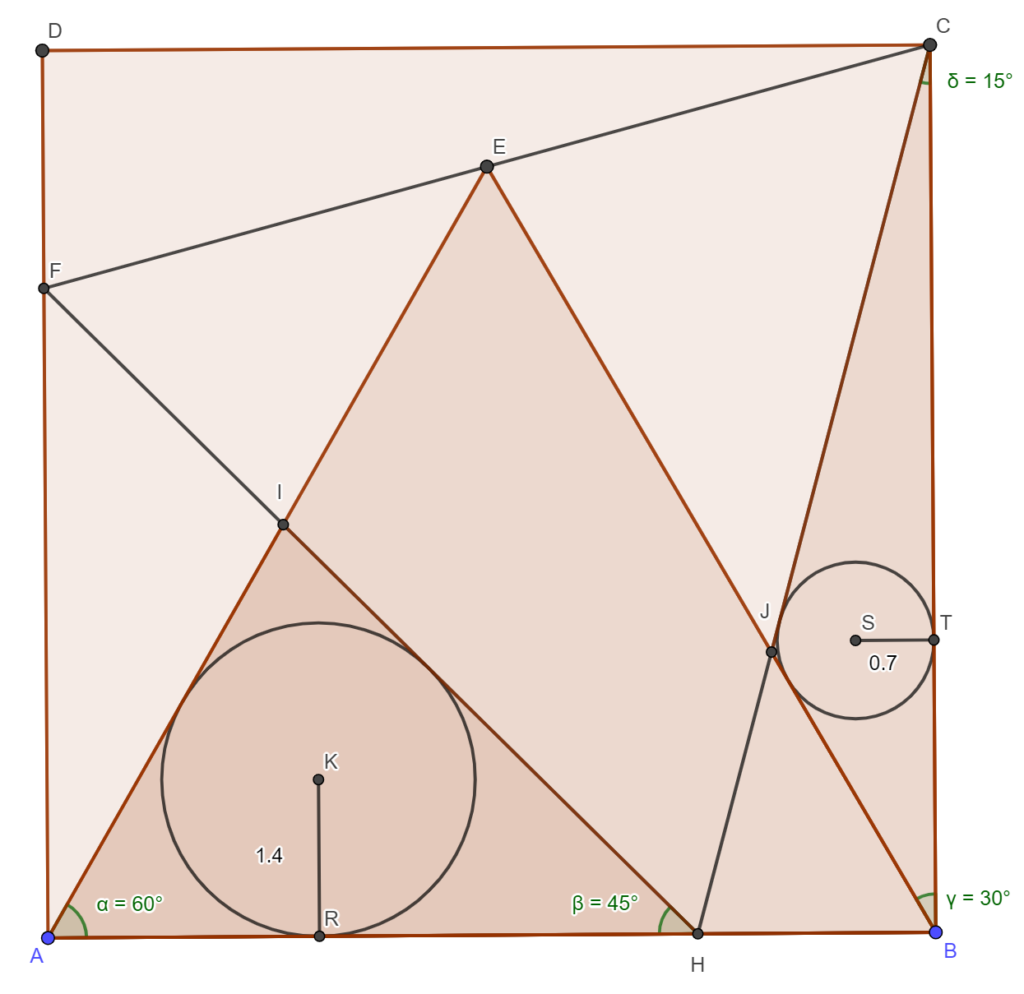
Uitleg
( frac{sin(x)}{cos(x)} )
Gegeven
ABCD is een vierkant. ΔABE en ΔCFH zijn gelijkzijdige driehoeken.
Te bewijzen
De stralen van de ingeschreven cirkels van ΔABE en ΔBJC verhouden zich tot elkaar als 2 : 1.
Bewijs:
We gebruiken een uitdrukking voor de grootte van de straat van de ingeschreven cirkel. Zie ( frac{sin(x)}{cos(x)} ).
