GH-04 Cirkels en raaklijnen
GH-04 Cirkels en raaklijnen
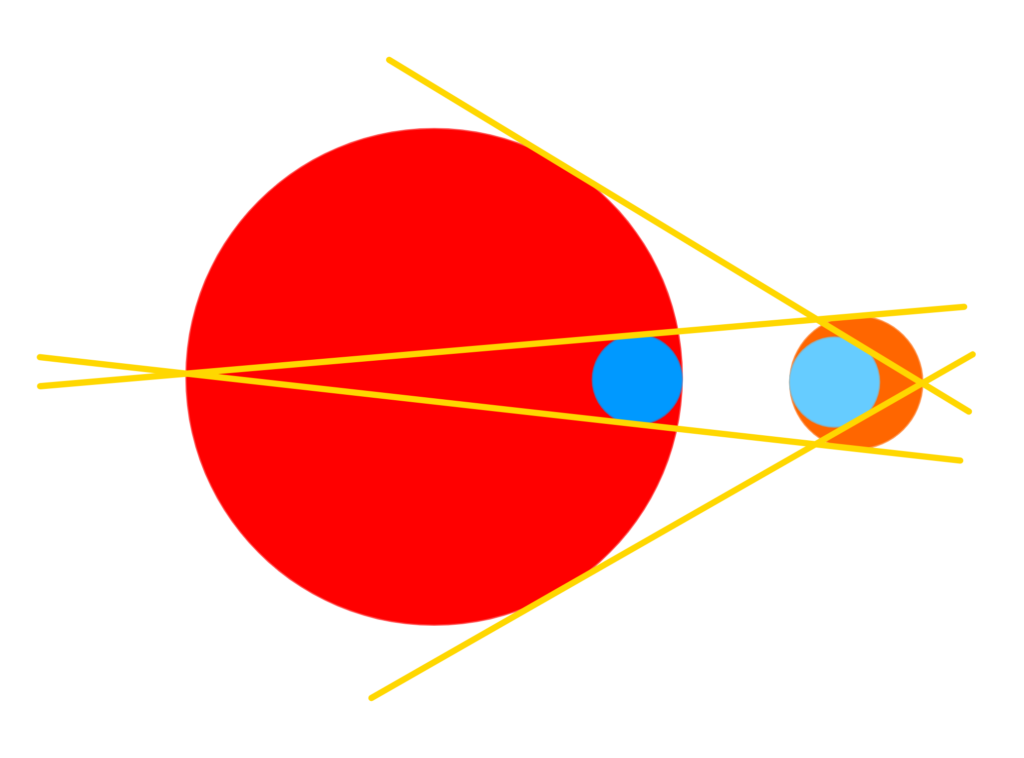
Er worden twee cirkels getekend (een rode en een orangje) die elkaar niet overlappen. Vanuit een punt op de linker cirkel worden twee raaklijnen aan de rechter cirkel getrokken. Vanuit een punt op de rechter cirkel worden twee raaklijnen aan de linker cirkel getrokken. Twee kleine cirkels (donker en lichtblauw) worden getekend raken aan de linker cirkel en de raaklijnen. Zie de tekening voor toelichting. Wat is het verband tussen de stralen van de cirkels?
Er geldt: de stralen van de twee kleine cirkels (donker en licht blauw) zijn gelijk, dus
( r_{3}=r_{4})
Bewijs
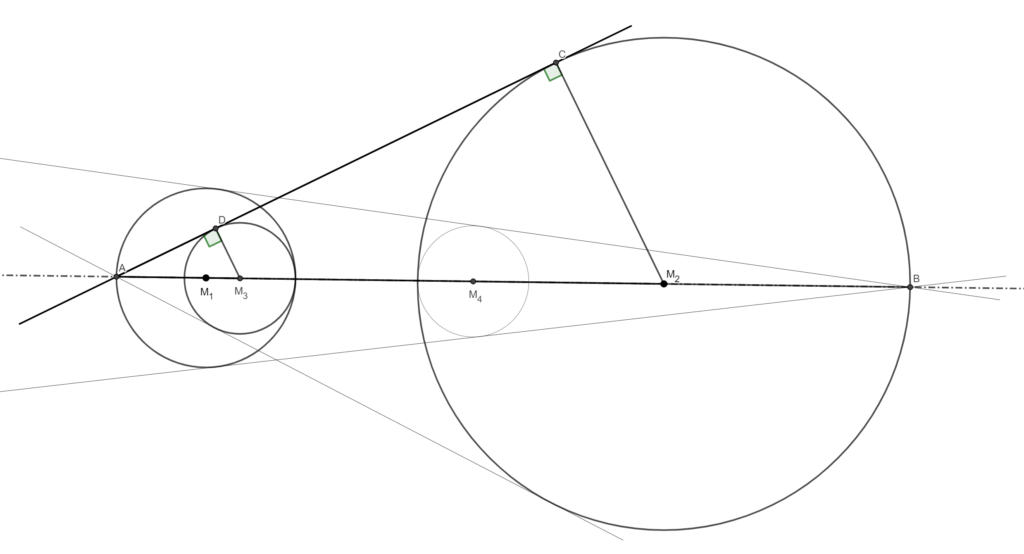
AD raakt de cirkel met middelpunt ( M_{3} ) dus geldt: ( M_{3}D⊥AD ) en AC raakt de cirkel met middelpunt ( M_{2} ) dus ( M_{2}C⊥AC ) (zie de hulpstelling 1).
ΔAM_{3}D ∼ ΔAM_{2}C, want deze driehoeken hebben beiden een rechte hoek en hebben ∠A gemeenschappelijk.
Daarom geldt: ( frac{M_{3}D}{M_{2}C}=frac{AM_{}}{AM_{2}} ).
We kunnen dit schrijven in termen van lengte van AB en stralen van de cirkels als volgt: ( frac{r_{3}}{R_{2}}=frac{2R_{1}-r_{1}}{AB-R_{2}}).
We gebruiken deze gelijkheid om een uitdrukking voor ( r_{3} ) te vinden.
(r_{3}(AB-R_{2})=R_{2}(2R_{1}-r_{3}) ) dus ( r_{3}AB-r_{3}R_{2}=2R_{1}R_{2}-r_{3}R_{2} ) dus ( r_{3}=frac{2R_{1}R_{2}}{AB} )
Op dezelfde manier is een identieke uitdrukking voor ( r_{4} ) te vinden: ( r_{4}=frac{2R_{1}R_{2}}{AB} ).
Hieruit volgt: ( r_{3}=r_{4} ) en dit moesten we bewijzen.
