GH-03 Drie cirkels tussen twee evenwijdige lijnen
GH-03 Drie cirkels tussen twee evenwijdige lijnen
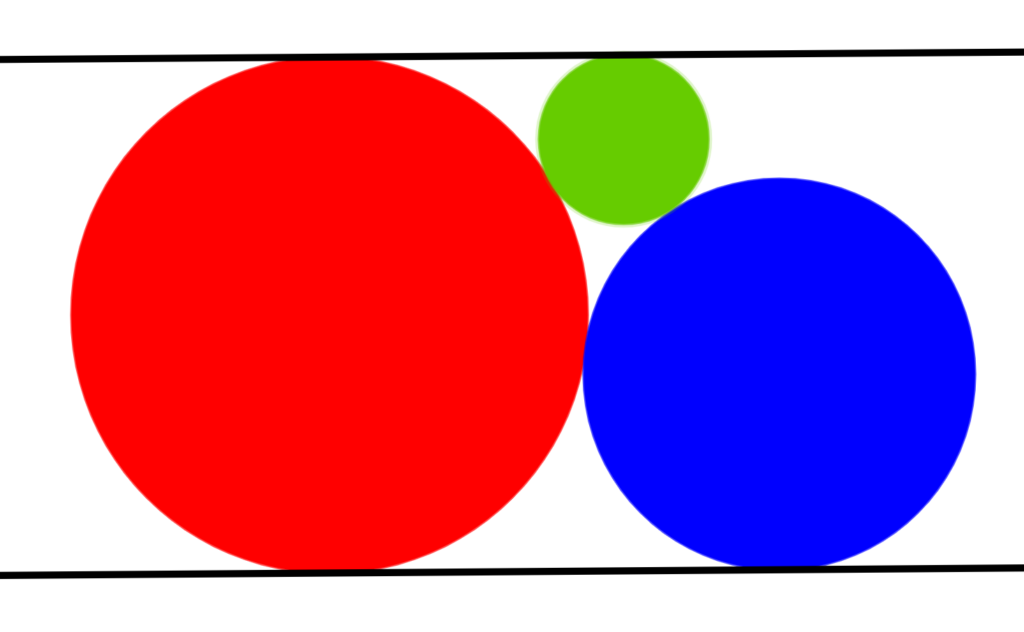
Tussen twee evenwijdige lijnen is een rode cirkel ingeklemd. Een blauwe cirkel raakt de onderste lijn en de rode cirkel. Er wordt een derde (groene) cirkel getekend die raakt aan de rode en de blauwe cirkel en aan de bovenste lijn.
Welk verband bestaat tussen de stralen van de cirkels?
Er geldt:
(r_{1}=sqrt{r_{2}r_{3}})
Bewijs
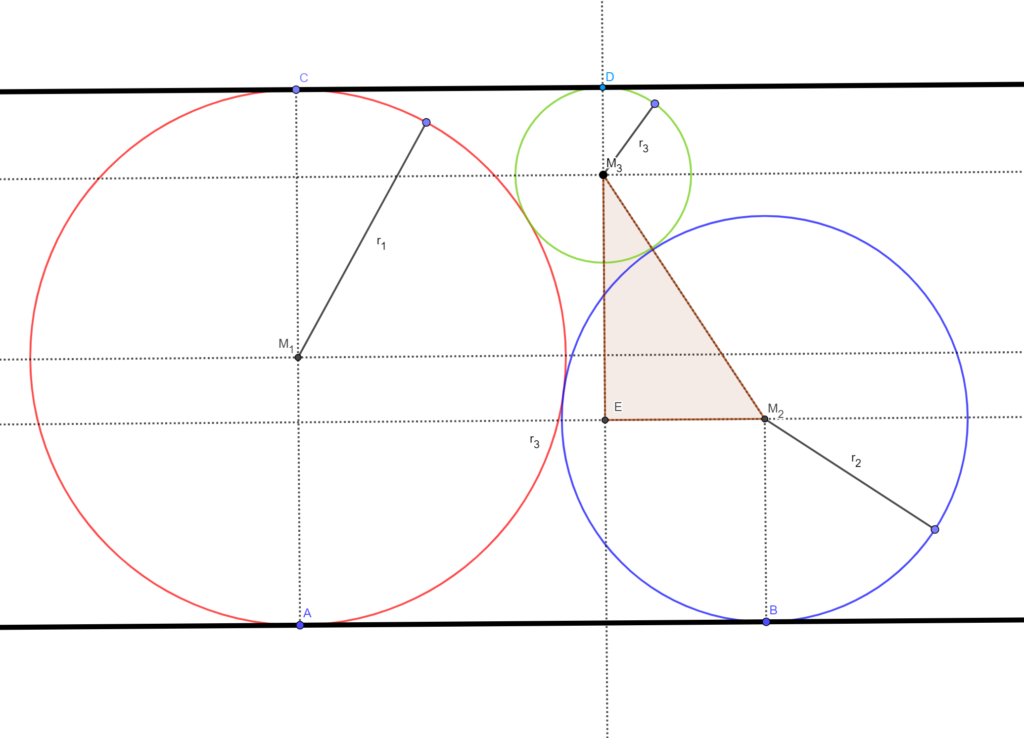
Merk op dat volgens sangaku GH-01 er geldt:
( AB=2sqrt{r_{1}r_{2} }) en ( CD=2sqrt{r_{1}r_{3}} ).
In ( Delta FM_{2}M_{3} ) geldt de stelling van Pythagoras, want ∠F=90°. Dus:
(1) ( FM_{2}^2+FM_{3}^2=M_{1}M_{2} )
Verder geldt:
(2) ( FM_{2}=EM_{2}-EF=AB-CD=2sqrt{r_{1}r_{2}}-2sqrt{r_{1}r_{3}} )
(3) ( FM_{3}=EG=AD-EA-GD=2r_{1}-r_{2}-r_{3} )
(4) ( M_{1}M_{2}=r_{1}+r{2} )
We substitueren uitdrukkingen (2), (3) en (4) in de vergelijking (1). Dat geeft:
( (2sqrt{r_{1}r_{2}}-2sqrt{r_{1}r_{3}})^2+(2r_{1}-r_{2}-r_{3})^2=(r_{1}+r{2})^2 )
Verdrijf nu de haakjes en werk verder uit:
(4r_{1}(sqrt{r_{2}}-sqrt{r_3})^2+(2r_{1}-r_{2}-r_{3})^2=(r_{2}+r_{})^2 )
(4r_{1}(sqrt{r_{2}}-sqrt{r_3})^2+4r_{1}^2-4r_{1}(r_{2}+r_{3})+(r_{2}+r_{3})^2=(r_{2}+r_{3})^2 )
(4r_{1}(sqrt{r_{2}}-sqrt{r_3})^2+4r_{1}^2-4r_{1}(r_{2}+r_{3})=0 )
((sqrt{r_{2}}-sqrt{r_3})^2+r_{1}-(r_{2}+r_{3})=0 )
(r_{2}-2sqrt{r_{2}r_{3}}+r_{3}+r_{1}-r_{2}-r_{3}=0 )
(r_{1}=2sqrt{r_{2}r_{3}})
Dit is precies wat we moesten bewijzen!
