GH-11 Twee cirkels en een halve cirkel

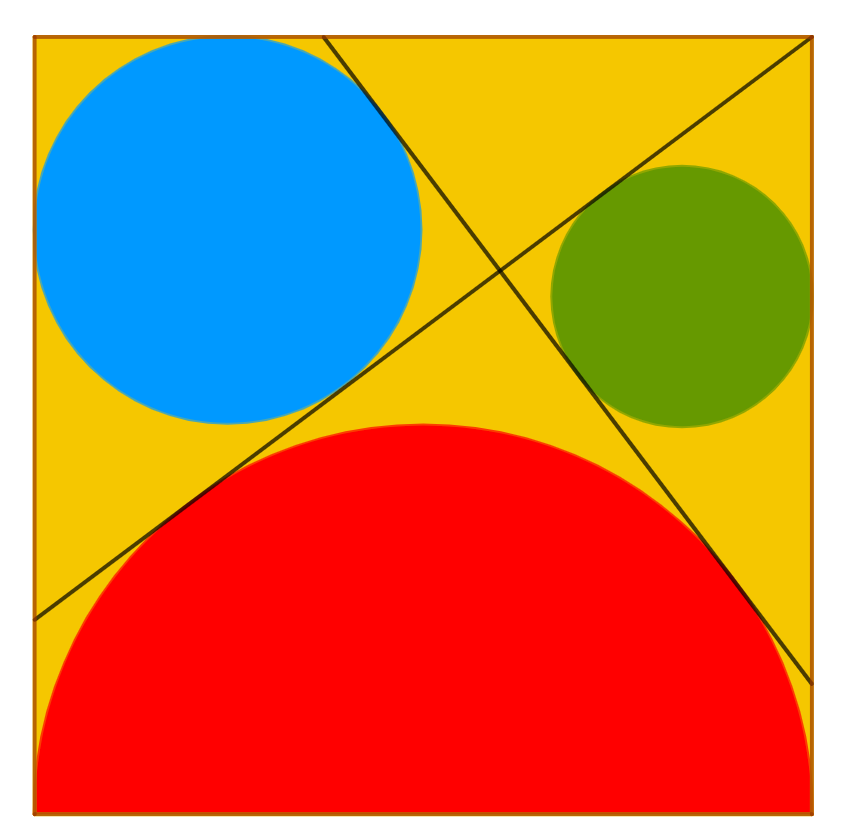
In een vierkant wordt een halve cirkel (rood) getekend met de basis van het vierkant als diameter. Vanuit het hoekpunt rechtsboven wordt een raaklijn aan deze halve cirkel getekend. Er ontstaat een driehoek linksboven in het vierkant. In deze driehoek wordt de ingeschreven cirkel (blauw) getekend. Dan wordt de gemeenschappelijke raaklijn aan deze cirkel en aan de halve cirkel getekend. In de driehoek gevormd door twee getekende raaklijnen en de rechter zijde van het vierkant wordt eveneens de ingeschreven cirkel getekend (groen).

Wat is de verhouding tussen de lengte van de stralen van de ingeschreven (blauwe en groene) cirkels?