GH-15 Opkomende zon

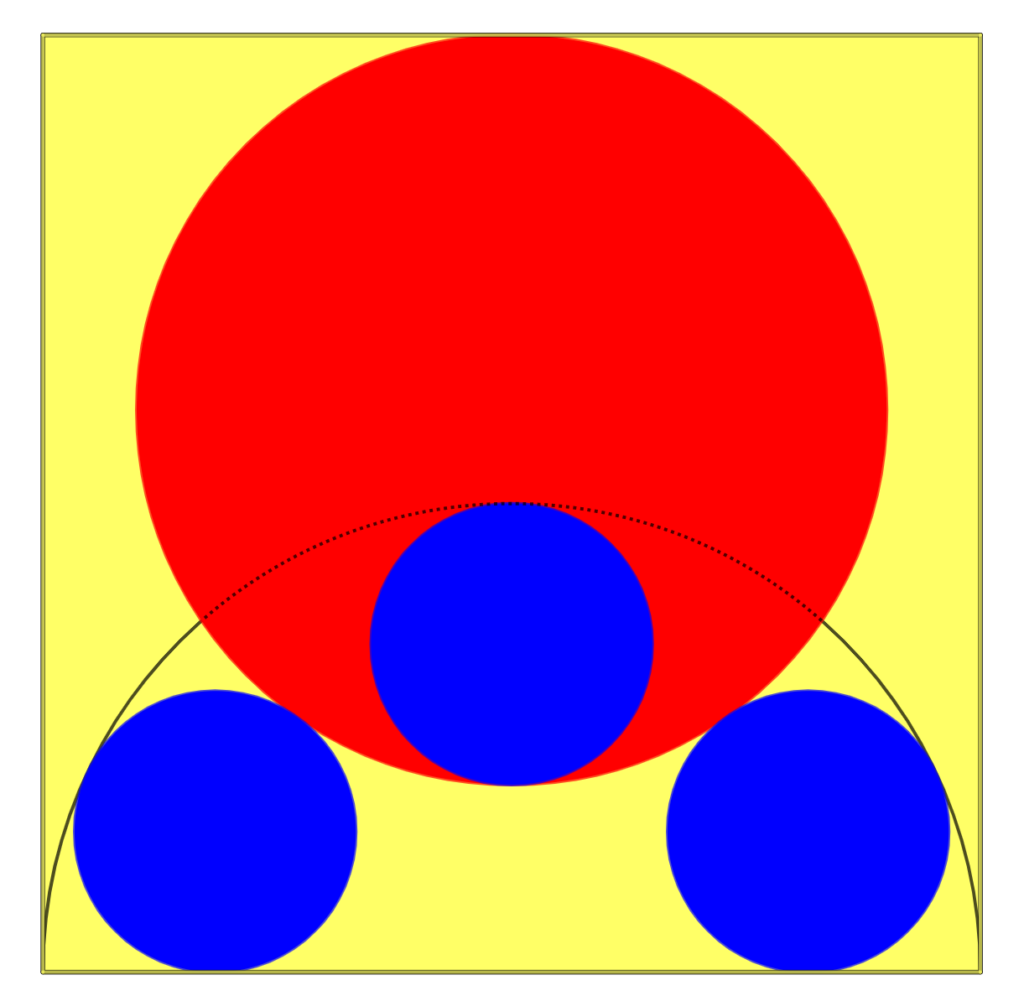
In en vierkant wordt een halve cirkel getekend met de basis van het vierkant als diameter. Er wordt in het vierkant ook een cirkel getekend (rood) waarvan het middelpunt ligt op de verticale lijn die het vierkant in twee gelijke delen verdeelt. Binnen de halve cirkel zijn drie (blauwe) cirkels getekend. Twee van deze cirkels raken aan de basis van het vierkant, aan de halve cirkel en aan de (rode) cirkel die eerder al werd getekend. De derde (blauwe) cirkel ligt binnen de rode cirkel, het middelpunt ligt op de verticale lijn die het vierkant in twee gelijke delen verdeelt en raakt aan de rode cirkel. Nu is lengte van de straal van de rode cirkel zo gekozen dat de straal van de drie blauwe cirkels even groot is. 

Wat is de verhouding tussen de lengte van de straal van de rode cirkel en de lengte van de straal van de blauwe cirkel?