Hulpstellingen

Ingeschreven cirkel in een rechthoekige driehoek

Stelling 2a

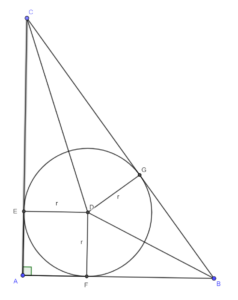
In rechthoekige \( \Delta \)ABC is de ingeschreven cirkel getekend. Voor de lengte van de straal r van deze cirkel geldt:

\( r=\frac{AB+AC -BC}{2} \)

Bewijs:

Er geldt: \( BF=BG, CE=CG \). Daarom is \( BC=BG+GC=BF+CE=AB-r+CA-r=AB+AC-2r \).

Omschrijven van deze vergelijking levert op: \( r=\frac{AB+AC -BC}{2} \)

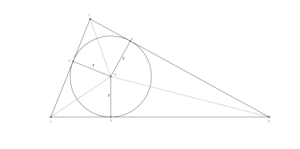
In \( \Delta \)ABC is de ingeschreven cirkel getekend. Voor de lengte van de straal r van deze cirkel geldt:

\( opp \Delta ABC =r\cdot omtrek \Delta ABC \) .