
- Beschrijving
- Curriculum
In deze cursus worden een aantal sangaku’s getoond. In opgaven ondersteund door Algebrakit kun je proberen de waarheid achter de tekening te achterhalen en aan te tonen welke bijzondere eigenschap er in het plaatje verborgen zit.
-
101-Wasan
Wasan - een sangaku met twee cirkels die elkaar raken en beiden een rechte lijn raken.
-
202 - De drie cirkels
Deze sangaku gaat over drie cirkels die op een lijn liggen en elkaar raken.
-
303 - Drie cirkels tussen twee stokjes
a
-
404 - Cirkels en stokjes
De Sangaku 04 - Cirkels en stokjes gaat over het verband tussen de stralen van twee cirkels die worden ingeklemd tussen stokjes en cirkels!
-
505 - Drie cirkels in een rechthoekige driehoek
In een rechthoekige driehoek wordt vanuit het hoekpunt met een rechte hoek een loodlijn op de overstaande zijde neergelaten (hoogtelijn). Er zijn nu drie rechthoekige driehoeken. In de drie rechthoekige driehoeken wordt de ingeschreven cirkel getekend. Wat is het verband tussen de lengte van de hoogtelijn en de stralen van de cirkels?
-
606 - Drie cirkels in een gelijkzijdige driehoek
Een Sangaku over een drietal cirkels in een gelijkzijdige driehoek.
-
707 - Vijf cirkels in een vierkant
Dit is een Sangaku over vijf cirkels in een vierkant.
-
808 - Zes cirkels in een rechthoek
In deze Sangaku zie je zes even grote cirkels ingeklemd in een rechthoek. We willen de lengte van de rechthoek en de breedte van de rechthoek uitdrukken in de straal van de cirkels.,
-
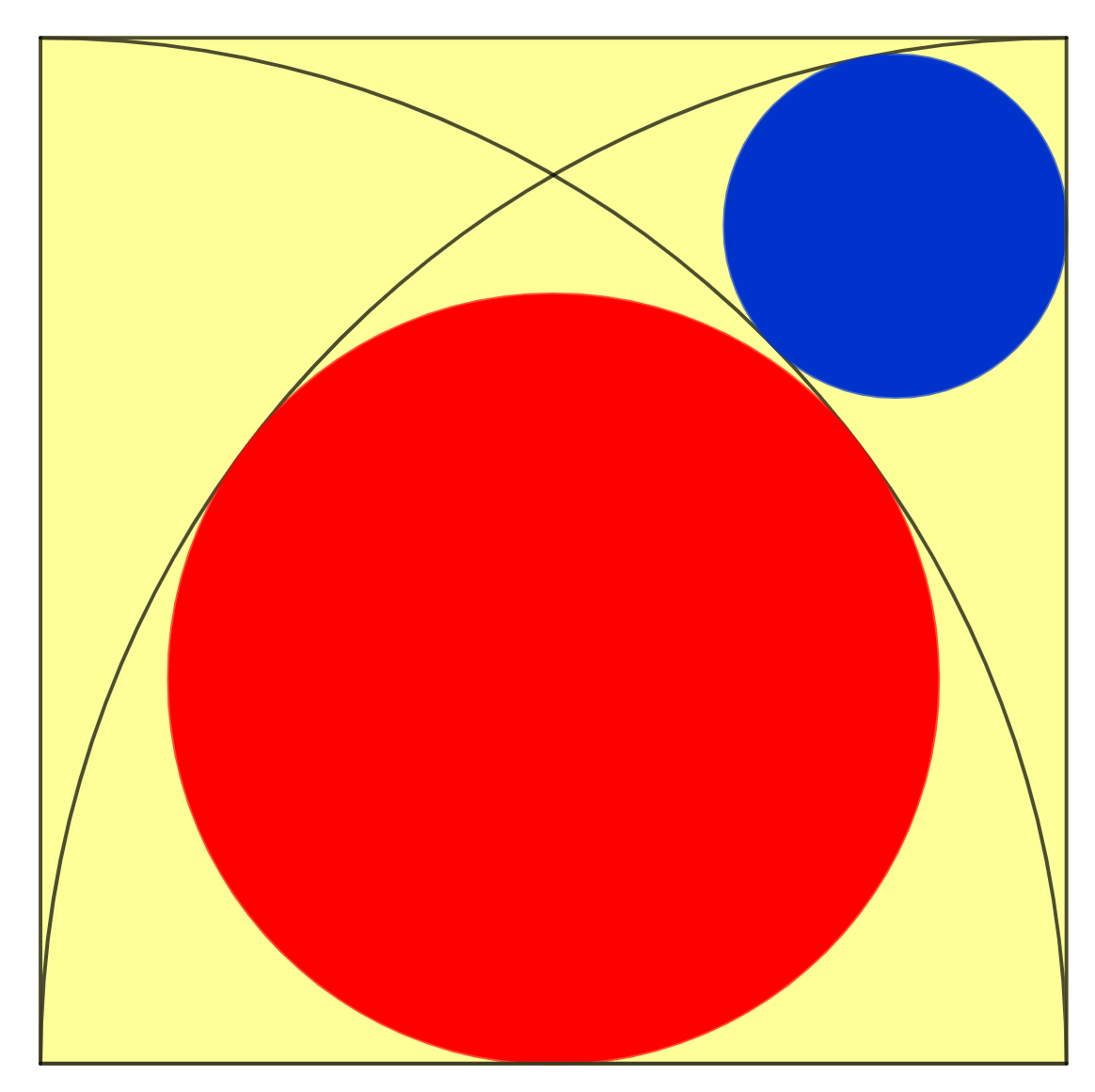
909 - De gotische boog
Een Sangaku waarbij, als in een gotische boog, twee kwart cirkels in een vierkant zijn getekend en twee cirkels worden ingeklemd in de figuur.
-
1010 - De gotische boog (II)
Een sangaku over cirkels en vierkant in een vierkant. De afbeelding lijkt op een gotische boog.
-
1111 - Twee cirkels en een halve cirkel
In een vierkant worden op een bepaalde manier een halve cirkel en twee cirkels getekend. Gevraagd wordt wat de verhouding is tussen de stralen van de cirkels.,
-
1212 - Het vierkant is in tweeën verdeeld
Een sangaku over drie cirkels in een vierkant. Wat is het verband tussen de stralen?
-
1313 - Drie cirkels in een vierkant
Deze sangaku gaat over drie cirkels in een vierkant.
-
1414 - Twee gelijke cirkels in een vierkant
Deze Sangaku gaat over een vierkant dat door een diagonaal in twee gelijke delen is verdeeld. Een helft van het vierkant wordt verdeeld in twee driehoeken waarin de ingeschreven cirkels gelijke straal hebben. Wat is dan de verhouding tussen de lengte van die straal en de zijde van het vierkant?
-
1515 - De rijzende zon
Deze sangaku lijkt op een plaatje van de rijzende zon. Er staan in een vierkant een grote en drie kleine congruente cirkels getekend. Er wordt gezocht naar de verhouding tussen de lengte van de straal van de grote cirkel en de lengte van de straal van de kleine cirkel.
-
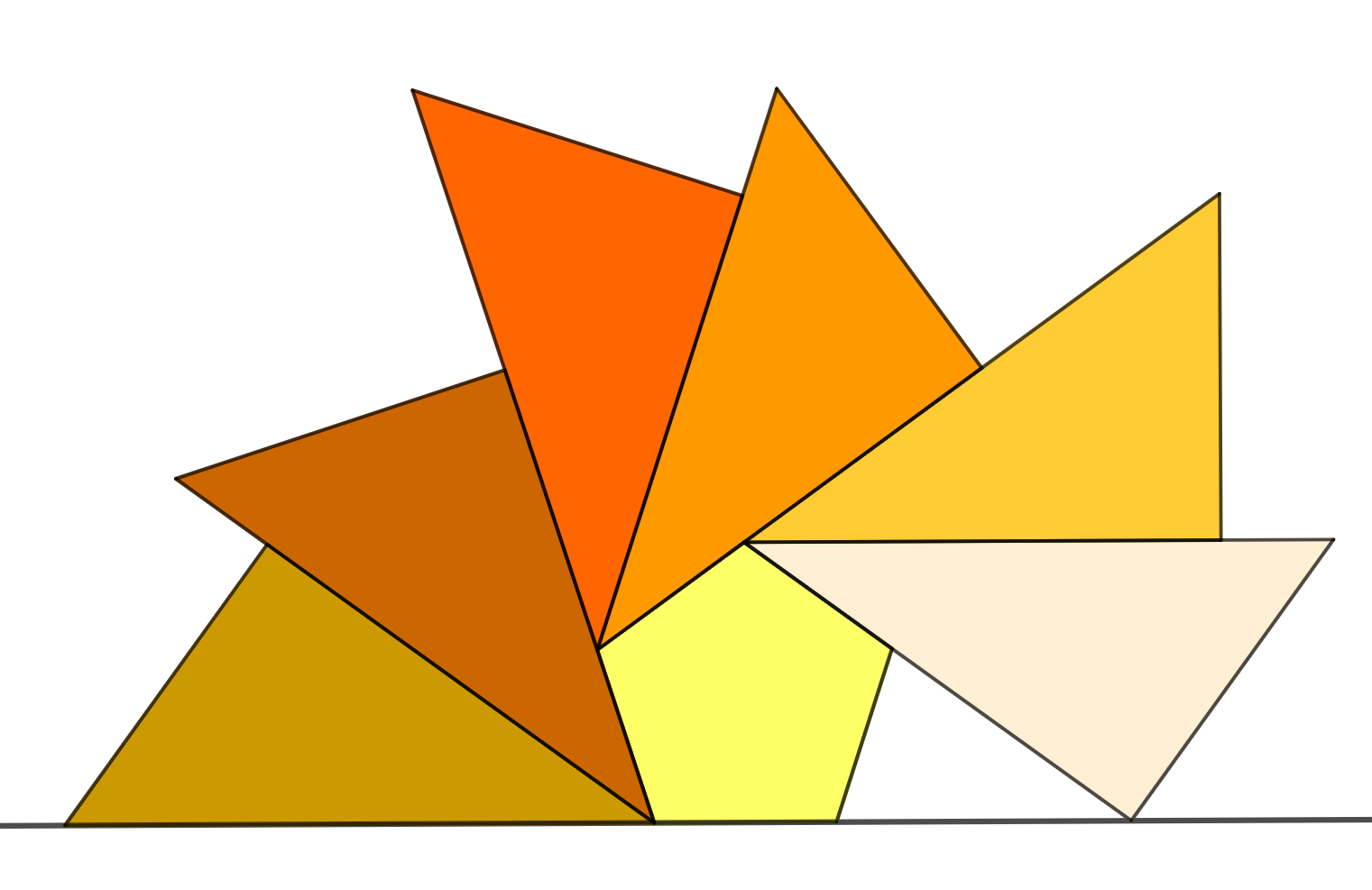
1616 - De waaier van rechthoekige driehoeken om een regelmatige vijfhoek
Om een regelmatige vijfhoek zijn een zestal rechthoekige driehoeken getekend. Deze driehoeken zijn congurent. Onderzocht wordt welke verhouding er bestaat tussen de hypothenusa van de driehoeken en de zijde van de regelmatige vijrfhoek.
-
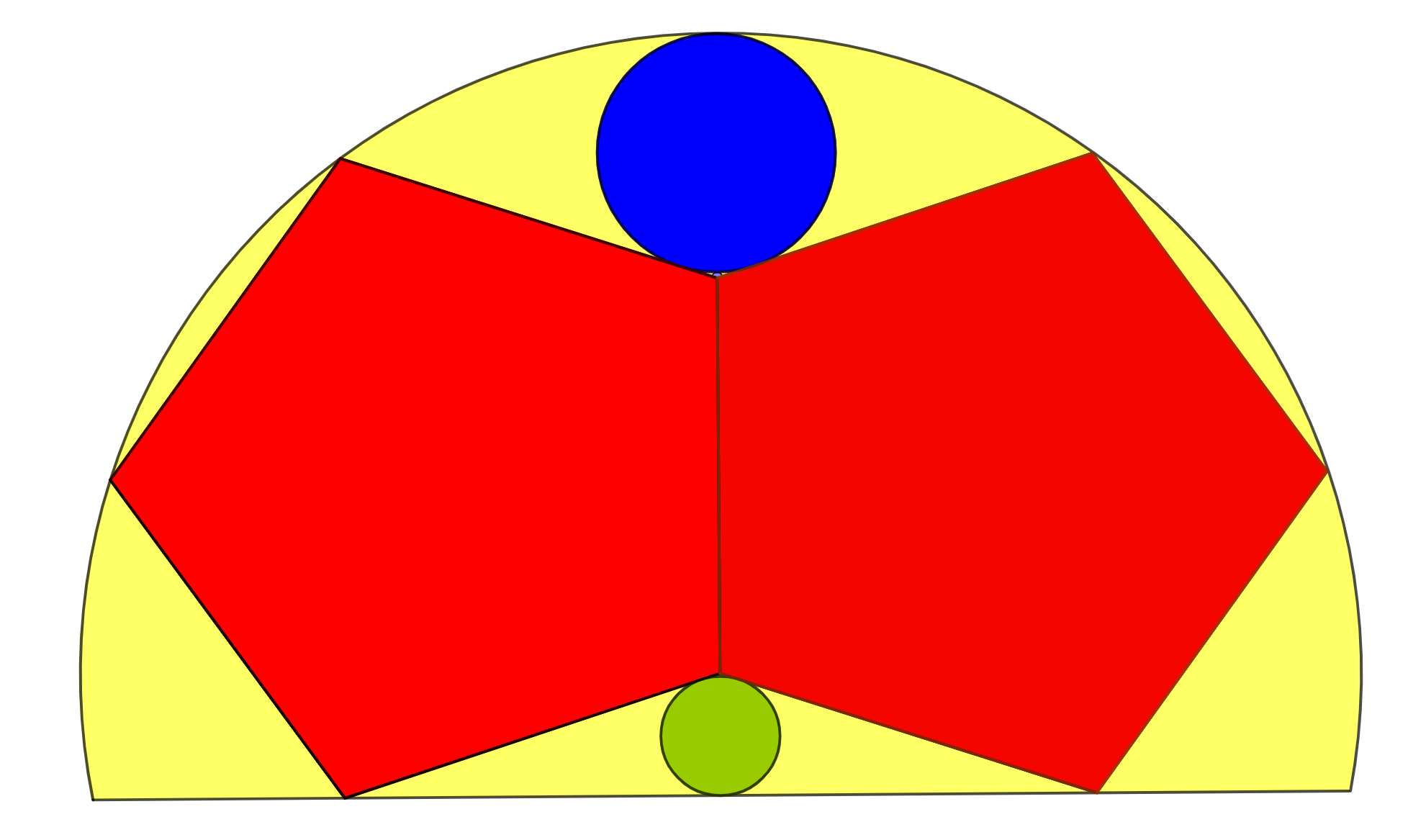
1717 - Twee regelmatige vijfhoeken
Deze sangaku gaat over twee cirkels die zijn ingeklemd tussen twee regelmatige vijfhoeken in een halve cirkel.
-
1818 - Origami en Sangaku
Een sangaku waarbij origami een rol speelt!
-
1919 - Stapel vierkanten
In een rechthoekige driehoek waarin drie vierkanten zijn getekend wordt een verband tussen stralen van ingeschreven cirkels bepaald.
-
2020 - Het probleem van de twee cirkels
In een vierkant worden twee gelijkzijdige driehoeken getekend. Tussen de lengte van de stralen van twee ingeschreven cirkels wordt een verband bewezen.
-
2121 - Het gelijkbenige trapezium
In deze sangaku wordt een gelijkbenig trapezium met een ingeschreven cirkel verdeeld in twee driehoeken door een diagonaal. In de twee driehoeken worden ingeschreven cirkel getekend. Welk verband is er tussen de stralen van de drie cirkels?
-
2222 - Een constante som
Deze sangaku gaat over een gelijkzijdige driehoek met een lijn door de top waarbij een beide kanten een rakende cirkel wordt getekend. De cirkel raakt aan driehoek, zijn door de top en lijn door de basis. De som van de stralen van deze twee cirkels blijkt constant te zijn.
-
2323 - Vier cirkels in een driehoek
In een driehoek wordt de ingeschreven cirkel getekend. In de overblijvende drie delen van de driehoek worden cirkels getekend die raken aan de ingeschreven cirkel en aan steeds twee zijden van de driehoek. Er wordt gevraagd een verband tussen de stralen van de vier cirkels te bewijzen.
-
2424 - Twee rechthoekige driehoeken en vijf cirkels
In een driehoek wordt de ingeschreven cirkel getekend. Dan worden op een bepaalde manier twee rechthoekige driehoeken getekend. In de figuur worden dat vier ingeschreven cirkels getekend en een verband tussen de stralen van die cirkels wordt bewezen.
-
2525 - Drie cirkels die twee aan twee aan elkaar raken
In een cirkel wordt een koorde getekend. Onder de koorde wordt een cirkel getekend die raakt aan de koorde en aan de cirkel en waarvan het middelpunt op de diameter ligt die loodrecht staat op de koorde. Dan worden op een bepaalde manier drie cirkel boven de koorde getekend. Er wordt gevraagd een bepaald verband tussen de lengten van de stralen aan te tonen.
-
2626 - De stelling van d'Ohara
In deze Sangaku wordt de stelling van d'Ohara behandeld.
-
2727 - Een ellips, een vierkant en een cirkel
Een sangaku over een ellips, een vierkant en een cirkel
-
2828 - De ellips en de halve cirkel
In een ellips wordt een halve cirkel getekend die raakt aan de ellips en waarvan de eindpunten van de diameter liggen op de ellips. In de delen buiten de halve cirkel die binnen de ellips liggen worden cirkels getekend die raken aan de ellips en aan de halve cirkel. Er moet worden bewezen dat een bepaald verband geldt tussen de stralen van de cirkels.
-
2929 - Een keten van cirkels in een ellips
In een ellips worden op een bepaalde wijze een keten van cirkels getekend. Er wordt een formule gegeven voor het verband tussen de straal van een cirkel uit de keten en de helft van de lengte van de lange as van de ellips.
-
3030 - Een ellips en vier rakende cirkels
Deze sangaku gaat over een ellips waarin op een bepaalde manier vier even grote cirkels zijn getekend. We bewijzen een formule voor de staal van die cirkels, uitgedrukt in de lengte van de halve as van de ellips.
-
3131 - Een kubus en drie bollen
In een bol zijn een kubus en drie bollen getekend. Er wordt gevraagd een formule te bewijzen voor de verhouding tussen de straal van de grootste bol en de straal van de kleinste bol.
-
3232 - Negen bollen
Op een vlak wordt een grote bol gelegd. Om de bol worden achtereenvolgens 8 even grote bollen op het vlak gelegd die allen de grote bol raken en elkaar steeds raken. Voor de verhouding tussen de straal van de grote bol en een kleine bol wordt een formule opgesteld.
-
3333 - De koepel
In een halve bol zijn een kubus en een bol geplaatst. Er wordt naar het verhouding tussen de straal van de halve bol en de bol gevraagd.
-
3434 - Bollen in een piramide
In deze sangaku wordt een piramide met vierkant grondvlak bekeken. Er worden vijf rakende bollen in getekend en een verband tussen de stralen bepaald.
-
351. De ingeschreven cirkel in een driehoek
In deze les leer je de formule voor de lengte van de straal van de ingeschreven cirkel in een rechthoek.
-
362. De ingeschreven cirkel in een rechthoekige driehoek
In deze les leer je een formule voor de straal van de ingeschreven cirkel in een rechthoekige driehoek.
-
373. De ingeschreven cirkel in een gelijkbenige driehoek.
In deze les leer je een formule voor de lengte van de straal van de ingeschreven cirkel in een gelijkbenige driehoek.
-
384. Een ingeschreven vierkant in een rechthoekige driehoek.
In deze les leiden we een formule af voor de lengte van de zijden van een vierkant waarvan de hoekpunten op de zijden van de driehoek liggen.
-
395. Een stelling over raaklijnen aan twee elkaar niet snijdende cirkels
In deze les leer je een verband tussen raaklijnen aan twee elkaar niet snijdende cirkels.
-
406. Een ingeschreven cirkel in een trapezium
In deze theorie wordt de lengte van de straal van de ingeschreven cirkel in een trapezium beschreven in termen van de zijden en de hoogte van het trapezium.
-
417. De lengte van de diagonaal in een regelmatige vijfhoek
In deze les leiden we een formule af voor de lengte van de diagonaal van een regelmatige vijfhoek.
-
428 Exacte waarden voor enkele goniometrische verhoudingen
In deze les geven we een aantal exacte waarden van goniometrische verhoudingen.
-
439. Goniometrische productformules
In deze les worden de goniometrische product formules behandeld. Deze formules heten ook wel de formules van Simpson, genoemd naar de Engelse wiskundige Thomas Simpson.
-
4410. Een rakende cirkel in een ellips
In deze les wordt een hulpstelling bewezen die gaat over een ellips waarin een cirkel met middelpunt op de lange as en die raakt boven- en onderkant van de ellips is getekend.
-
4511. Raaklijnen vanuit een punt buiten de cirkel aan de cirkel
Deze stelling gaat over de raaklijnen vanuit een punt buiten de cirkel aan de cirkel.
