1. De ingeschreven cirkel in een driehoek

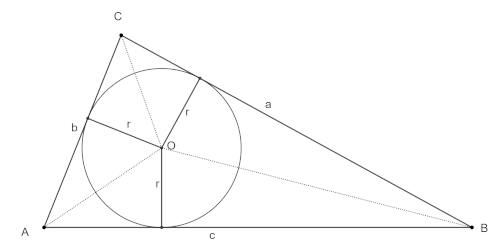
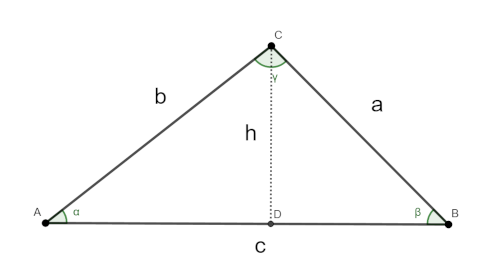
Stelling (deel 1)

De formule voor de lengte van de straal van de ingeschreven cirkel luidt:

\( r=\frac{1}{2} \sqrt{\frac{(-a+b+c)(a-b+c)(a+b-c)}{(a+b+c)}} \)

Bewijs

Er geldt: \( opp \Delta ABC = opp \Delta AOB + opp \Delta BOC + opp \Delta AOC  = \)

\( \frac{1}{2}rc + \frac{1}{2} ra + \frac{1}{2} rb = \frac{1}{2} r(a+b+c) \)

Dus \( r= \frac{2 \cdot opp \Delta ABC}{(a+b+c)} \)    FORMULE (1)

In figuur 2 lezen we af: \( sin(α)= \frac{h}{b} \) dus \( h=b \cdot sin(α) \) .

Volgens de cosinusregel geldt: \( a^{2} = b^{2} + c^{2} -2bc \cdot cos(α) \) .

Dus daarom is \( cos(α) = \frac{b^{2} + c^{2} – a^{2} }{2bc} \) . 

We werken nu een formule uit voor de oppervlakte van driehoek ABC. 

\( opp \Delta ABC = \frac{1}{2} h \cdot c = \frac{1}{2} b \cdot c \cdot sin(α)= \)

Dus \( opp \Delta ABC = \frac{1}{2}b \cdot c \cdot \sqrt{1-cos^{2}(α)} = \) 

\( = \frac{1}{2}b \cdot c \cdot \sqrt{(1+cos(α))(1-cos(α))} = \)

 \( = \frac{1}{2}b \cdot c \cdot \sqrt{(1+\frac{b^{2} + c^{2} – a^{2} }{2bc} )(1-\frac{b^{2} + c^{2} – a^{2} }{2bc} )} = \)

 \( = \frac{1}{2}b \cdot c \cdot \sqrt{\frac{(2bc+b^{2}+c^{2} – a^{2} )(2bc-b^{2}-c^{2} + a^{2} )}{(2bc)^{2}}} = \)

\( = \frac{1}{4} \sqrt{((b+c)^{2}-a^{2})(a^{2}-(b-c)^{2} )} = \)

\( = \frac{1}{4} \sqrt{(b+c+a)(b+c-a)(a+b-c)(a-b+c)} \)

Dit vullen we nu in in FORMULE (1) voor de straal r.

\( r=\frac{1}{2} \sqrt{ \frac{(b+c+a)(b+c-a)((a+b-c)(a-b+c)}{(a+b+c)^{2}}} \)

DUS: 

\( r= \frac{1}{2} \sqrt { \frac{(-a+b+c)(a-b+c)(a+b-c)}{(a+b+c)}} \)

En dit is precies de formule die we wilden bewijzen!!

figuur 1

figuur 2

Stelling (deel 2)

De formule voor de lengte van de straal van de ingeschreven cirkel luidt:

\( r=a\frac{sin(\frac{β}{2})sin(\frac{ɣ}{2})}{cos(\frac{α}{2})}\)

Bewijs

figuur 1

figuur 2