11. Raaklijnen vanuit een punt buiten de cirkel aan de cirkel

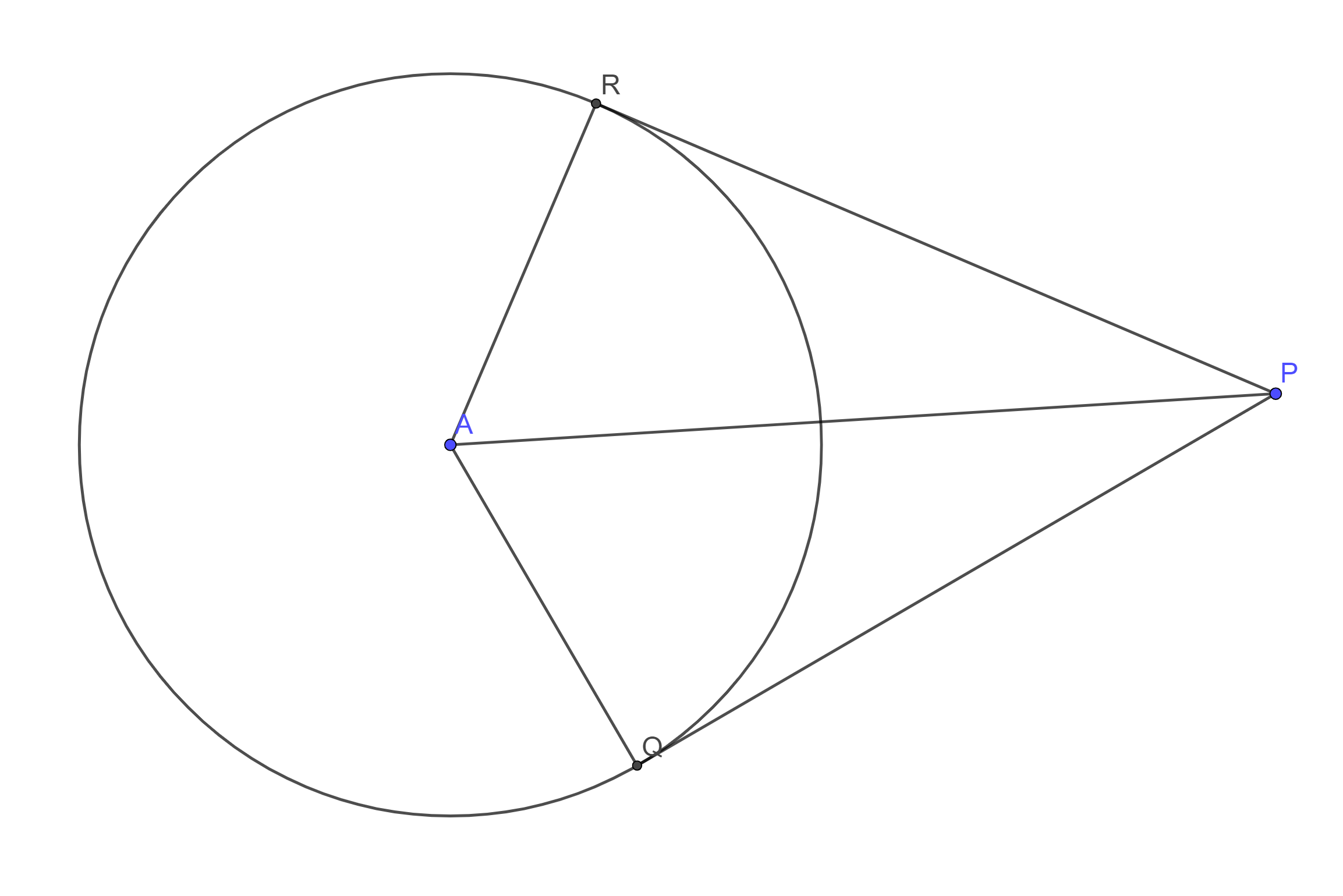
Stelling over raaklijnen aan een cirkel

Als vanuit een punt \( P \) buiten de cirkel de raaklijnen aan de cirkel de cirkel raken in \(Q\) en \(R\) dan geldt: \(PQ \, = \, PR \) .

Bewijs

Volgens de stelling van Thales geldt: \( \angle PRA \, = \, \angle PQA \, = \, 90 ^\circ \) .

Daarnaast geldt dat \( AR \, = \, AQ \) en natuurlijk geldt \( AP \, = \ AP \) .

Dus \( \Delta \, APR \, \cong \, \Delta \, APQ \).

Daar volgt uit dat \( PQ \, = \, PR \) .